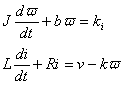Penggunaan program simulasi berbantuan komputer untuk memahami kerja suatu sistem kontrol semakin popular. Keuntungan nyata penggunaan komputer dalam memahami sistem tersebut adalah mempermudah kerja karena tidak membutuhkan berbagai peralatan seperti alat ukur, generator fungsi, osiloskop, kabel konektor, sumber daya, protoboard untuk merealisasi sistem untuk dianalisa. Kita dapat menentukan parameter kontrol yang sesuai sebelum merealisasi sistem tersebut. Tulisan ini akan membahas penggunaan simulink pada Matlab dalam merancang sistem kontrol PID pada motor DC.
PENDAHULUAN
Perkembangan teknologi kontrol mengalami banyak perkembangan dari kontrol konvensional ke kontrol otomatis sampai kontrol cerdas. Demikian juga perkembangan teknologi komputer terus berkembang seiring perkembangan teknologi elektronika yang semakin maju. Sistem kontrol dibutuhkan untuk memperbaiki tanggapan sistem dinamika agar didapat sinyal keluaran seperti yang diinginkan. Untuk dapat merancang sistem kontrol yang baik diperlukan analisis untuk mendapatkan gambaran tanggapan sistem terhadap aksi pengontrolan. Sebelum merancang sistem kontrol, kita harus memodelkan sistem dinamika terlebih dahulu. Permasalahan yang dihadapi dalam merancang sistem kontrol adalah mendapatkan fungsi alih dari sistem tersebut dengan pendekatan matematika kemudian menganalisisnya apakah sistem tersebut sudah baik atau belum. Dengan bantuan matlab proses analisa fungsi alih akan menjadi jauh lebih mudah dan cepat sehingga akan lebih memudahkan dalam merancang suatu sistem kontrol. Hal lebih lanjut adalah melihat respon keluaran sistem tersebut terhadap gangguan yang ada.
Permasalahan yang akan dibahas pada laporan ini adalah bagaimana menganalisa pengaruh gangguan terhadap suatu sistem kontrol motor DC menggunakan simulink matlab.
TINJAUAN PUSTAKA
Pemodelan sistem
Motor DC diilustrasikan seperti Gambar 1 dimana input motor berupa tegangan suplai (ν) dan output adalah posisi rotasi (θ).

Gambar 1. Ilustrasi motor DC
Pada kasus kontrol ini yang digunakan adalah motor DC dengan parameter-parameter fisik motor sebagai berikut :
Moment inertia motor (J) =0.01 kg m2/s2
Damping ratio sistem mekanis (b) =0.1 Nms
Konstanta electromotive force (k=kt=ke)=0.01 Nm/A
Resistansi motor (R) = 1Ω
Induktansi motor (L) = 0.5 H
Torsi motor berhubungan dengan arus armature dengan faktor konstanta armature kt dan emf balik e berhubungan dengan kecepatan rotasi ω dengan factor konstanta motor ke.

Berdasarkan Gambar 1 diatas, dengan mengkombinasikan hukum Newton dan Kirchhoff dimana kt=ke= k maka dapat ditulis persamaan :
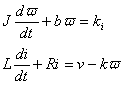
Hubungan antara kecepatan rotasi dan posisi rotasi adalah : 
Operasi transformasi Laplace pada persamaan diatas akan menghasilkan :
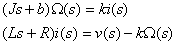
Selanutnya didapatkan fungsi alih yang merupakan perbandingan antara kecepatan rotasi terhadap tegangan input.

Model matematika motor DC pada simulink dapat dilihat pada Gambar 2.
Gambar 2. Model matematika motor DC pada simulink
Kontrol PID sering digunakan karena merupakan kontrol sistem tertutup yang cukup sederhana dan kompatibel dengan sistem kontrol lainnya seperti fuzzy, adaptif dan robust kontrol. Fungsi alih C(s) pada sistem kontrol PID merupakan besaran yang nilainya tergantung pada nilai konstanta dari sistem Proportional, Integral dan Derivative.

Sistem kontrol PID terdiri dari 3 buah cara pengaturan, yaitu kontrol P, I dan D dengan masing-masing memiliki kelebihan dan kekurangan. Dalam implementasinya masing-masing cara dapat bekerja sendiri ataupun gabungan diantaranya. Dalam perancangan sistem kontrol ini yang perlu dilakukan adalah mengatur parameter P, I dan D agar tanggapan sinyal keluaran sistem terhadap masukan tertentu sebagaimana yang diinginkan. Tanggapan sistem kontrol PID terhadap perubahan parameter P, I dan D dapat dilihat pada Tabel 1.
Tabel 1. Tanggapan sistem kontrol PID terhadap perubahan parameter P, I dan D
| Tanggapan Lup Tertutup | Waktu Naik | Overshoot | Waktu Turun | Kesalahan Keadaan Tunak |
| Proportional (KP) | Menurun | Meningkat | Perubahan kecil | Menurun |
| Integral (KI) | Menurun | Meningkat | Meningkat | Hilang |
| Derivative(KD) | Perubahan kecil | Menurun | Menurun | Perubahan kecil |
Untuk merancang sistem kontrol PID dilakukan dengan metode coba-coba atau trial and error dengan kombinasi antara P, I dan D sampai ditemukan nilai yang tepat untuk menghasilkan respon keluaran sistem seperti yang diinginkan karena parameter KP ,KI , dan KD tidak berdiri sendiri.
METODE PENELITIAN
Penganalisaan terhadap gangguan dapat dilakukan dengan memodelkan sistem motor DC, kontroler dan membuat simulasi tegangan referensi dan gangguan pada simulink matlab. Pada sistem ini gangguan diset terjadi pada detik ke-5 dengan besar gangguan konstan 2 V hingga seterusnya. Model dari sistem keseluruhan dapat dilihat pada Gambar 3. Model sistem motor DC dapat dilihat pada Gambar 4. Rancangan model kontroler PID yang digunakan dapat dilihat pada Gambar 5.
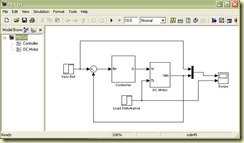
Gambar 3. Model simulasi sistem dengan simulink matlab

Gambar 4. Model sistem motor DC

Gambar 5. Rancangan model kontroler PID
HASIL DAN PEMBAHASAN
Tampilan osiloskop dari sinyal referensi, gangguan dan respon keluaran sistem kontrol dapat dilihat pada Gambar 6.

Gambar 6. Tampilan sinyal referensi, gangguan dan respon keluaran sistem kontrol
Dari respon keluaran sistem dapat dilihat bahwa saat terjadi gangguan pada detik ke-5 sebesar 2 Volt, sistem sedikit terganggu tetapi pada saat yang singkat sistem kembali pada keadaan semula seperti yang diinginkan yaitu saat referensi 10 Volt.
Kita dapat mengganti parameter Kp, Ki, dan Kd pada model kontroler PID untuk mendapatkan respon keluaran lain yang mungkin lebih baik.
SIMPULAN
Dari hasil penelitian ini dapat disimpulkan bahwa perancangan suatu sistem kontrol akan menjadi lebih mudah dan menarik dengan menggunakan bantuan program aplikasi komputer matlab dengan fasilitas simulink-nya.
SARAN
Setelah melihat dan menganalisis masalah yang dihadapi mahasiswa jurusan Teknik Elektro dalam mempelajari teori perkuliahannya, perlu disarankan penyediaan komputer khusus untuk simulasi dan analisis agar mereka lebih termotivasi mempelajari prinsip kerja suatu sistem yang cenderung membosankan karena tidak dapat mengetahui secara pasti keluaran yang semestinya dan melihat pengaruh input terhadap outputnya.
RUJUKAN
Djoko Purwanto, PhD. 2006. Perancangan Sistem Kontrol dengan Matlab. Surabaya, ITS.
Ogata, Katsuhiko. 1997. Teknik Kontrol Automatik Jilid I dan II, Edisi 2. Jakarta: Erlangga.
Stanley M.Shinners. 1998. Matlab and Simulink Based Books. Modern Control System Theory and Design, 2ed. New York: John Wiley &Sons,Inc.
Thomas Wahyu Dwi Hartanto dan Y.Wahyu Agung P. 2003. Analisis dan Desain Sistem Kontrol dengan Matlab. Yogyakarta: ANDI