SIMULASI SISTEM KONTROL PID UNTUK MOTOR DC DENGAN SIMULINK MATLAB

by: Henry Toruan

Pemodelan sistem

Motor DC diilustrasikan seperti Gambar 1 dimana input motor berupa tegangan suplai (ν) dan output adalah posisi rotasi (θ).

Gambar 1. Ilustrasi motor DC

Pada kasus kontrol ini yang digunakan adalah motor DC dengan parameter-parameter fisik motor sebagai berikut :

Moment inertia motor (J) =0.01 kg m²/s²

Damping ratio sistem mekanis (b) =0.1 Nms

Konstanta electromotive force (k=k_t=k_e)=0.01 Nm/A

Resistansi motor (R) = 1Ω

Induktansi motor (L) = 0.5 H

Torsi motor berhubungan dengan arus armature dengan faktor konstanta armature k_t dan emf balik e berhubungan dengan kecepatan rotasi ω dengan factor konstanta motor k_e.

Berdasarkan Gambar 1 diatas, dengan mengkombinasikan hukum Newton dan Kirchhoff dimana k_t=k_e= k maka dapat ditulis persamaan :

Hubungan antara kecepatan rotasi dan posisi rotasi adalah :

Operasi transformasi Laplace pada persamaan diatas akan menghasilkan :

Selanutnya didapatkan fungsi alih yang merupakan perbandingan antara kecepatan rotasi terhadap tegangan input.

Model matematika motor DC pada simulink dapat dilihat pada Gambar 2.

Gambar 2. Model matematika motor DC pada simulink

PENGANALISAAN SISTEM

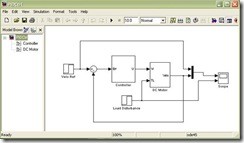
Penganalisaan terhadap gangguan dapat dilakukan dengan memodelkan sistem motor DC, kontroler dan membuat simulasi tegangan referensi dan gangguan pada simulink matlab. Pada sistem ini gangguan diset terjadi pada detik ke-5 dengan besar gangguan konstan 2 V hingga seterusnya. Model dari sistem keseluruhan dapat dilihat pada Gambar 3. Model sistem motor DC dapat dilihat pada Gambar 4. Rancangan model kontroler PID yang digunakan dapat dilihat pada Gambar 5. Tampilan osiloskop dari sinyal referensi, gangguan dan respon keluaran sistem kontrol dapat dilihat pada Gambar 6.

Gambar 3. Model simulasi sistem dengan simulink matlab

Gambar 4. Model sistem motor DC

Gambar 5. Rancangan model kontroler PID

Gambar 6. Tampilan sinyal referensi, gangguan dan respon keluaran sistem kontrol

Dari respon keluaran sistem dapat dilihat bahwa saat terjadi gangguan pada detik ke-5 sebesar 2 Volt, sistem sedikit terganggu tetapi pada saat yang singkat sistem kembali pada keadaan semula seperti yang diinginkan yaitu saat referensi 10 Volt.

KESIMPULAN

Berdasarkan hasil analisis dapat diambil kesimpulan sebagai berikut :

1. Penggunaan simulink pada matlab akan memudahkan untuk menganalisa sistem kontrol yang kompleks dan tampilan scope menjadikannya lebih menarik.
2. Dari hasil analisa untuk kasus diatas dapat dilihat bahwa dengan kontrol PID yang digunakan dapat mengembalikan kestabilan sistem ke keadaan awal pada saat ada gangguan yang kontinu.

DAFTAR PUSTAKA

1. Djoko Purwanto, PhD, (2006),”Perancangan Sistem Kontrol dengan Matlab”, Surabaya, ITS

2. Ogata, Katsuhiko, (1997), “Teknik Kontrol Automatik Jilid I dan II” Edisi 2, Jakarta, Erlangga

3. Stanley M.Shinners, (1998),”Matlab and Simulink Based Books. Modern Control System Theory and Design, 2ed, New York John Wiley &Sons,Inc.

4. Thomas Wahyu Dwi Hartanto dan Y.Wahyu Agung P., (2003), “Analisis dan Desain Sistem Kontrol dengan Matlab”, Yogyakarta, ANDI